大数据去重统计

Unique Visitor(UV)是大数据统计中常见一个指标，但由于其自身的不可加性，常常会碰见性能瓶颈。本文我们将对比几种常见计算UV的方法，了解其原理以及特点。

一点数学

基数(Cardinality)定义：一个集合中不同元素的个数

A = \{1, 3, 3, 5\} \Longrightarrow |A| = 3

当元素个数有限时，我们可以清楚地计算基数，但当元素个数无限时，奇怪的事就会发生，比如无穷 ∞ 和 ∞ + 1谁大？有兴趣的可以查看希尔伯特旅馆悖论

Set

实现：Java中提供Set数据结构存储不重复的元素集合
```
Set<Long> set = new HashSet<>(Arrays.asList(1L, 3L, 3L, 5L));
System.out.println(set.size())
```
- 这也是SQL中Count Distinct语法背后的实现方法
特点：
- 对任何数据类型都是绝对精确的
- 但存储占用大：一亿64位整数需要10000000 * 64 / (8 * 1024 * 1024) = 762.9MB
优化：虽然集合的存储计算消耗大，但我们也有很多方法去优化计算
- 一般我们是直接采取下列SQL计算用户数：
```
SELECT day, COUNT(DISTINCT user_id)
FROM T
GROUP BY day
```
- 但当有数据倾斜的时候，我们可以采用分桶优化：
```
SELECT day, SUM(cnt)
FROM (
    SELECT day, COUNT(DISTINCT user_id) as cnt
    FROM T
    GROUP BY day, MOD(HASH_CODE(user_id), 1024)
)
GROUP BY day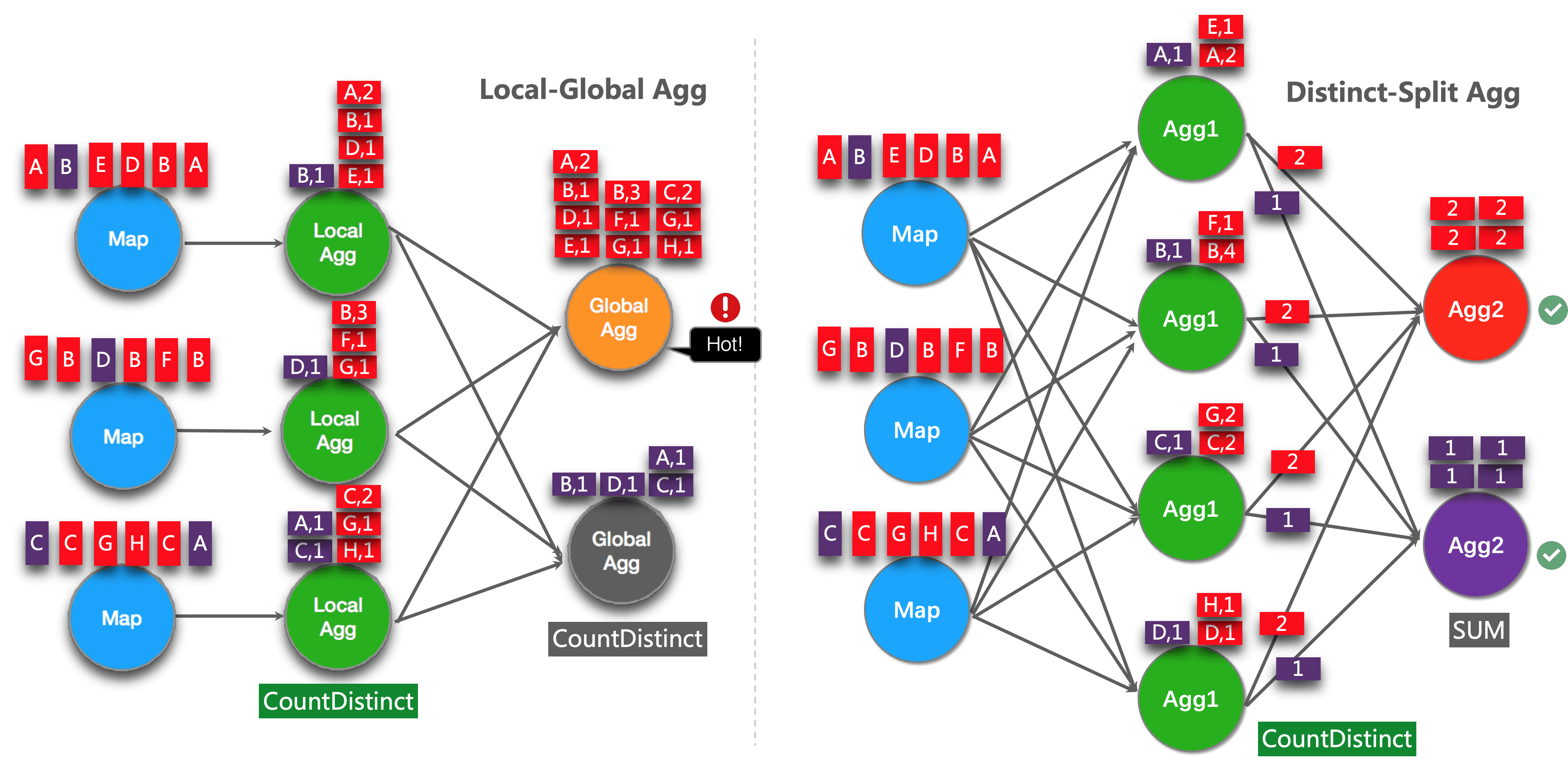
```

旁注: HashSet利用hashCode作为索引，如果hash冲突怎么办？参考Java HashMap

Bitmap

原理: Bitmap将具体数据映射到bit数组中，并将相应bit位设置为1
0
1
0
1
0
1
0
0

可见Bitmap可以利用位运算高效地进行合并统计

BitSet

实现：Java中提供BitSet数据结构

BitSet bitset = BitSet.valueOf(new long[] {1L, 3L, 3L, 5L})
System.out.println(bitset.cardinality())

特点
- 对整型数据结构完全精确，且占用空间小，一亿数据只需10000000 / （8 * 1024 * 1024）= 11.9MB
- 数据稀疏时空间浪费：存入1, 8888, 99999999这三个数据时，需要至少建立一个99999999长度的 BitMap，但是实际上只存了3个数据

RoaringBitmap

原理：将32整数按照高16位分桶，并将底16位放入相应的Container中
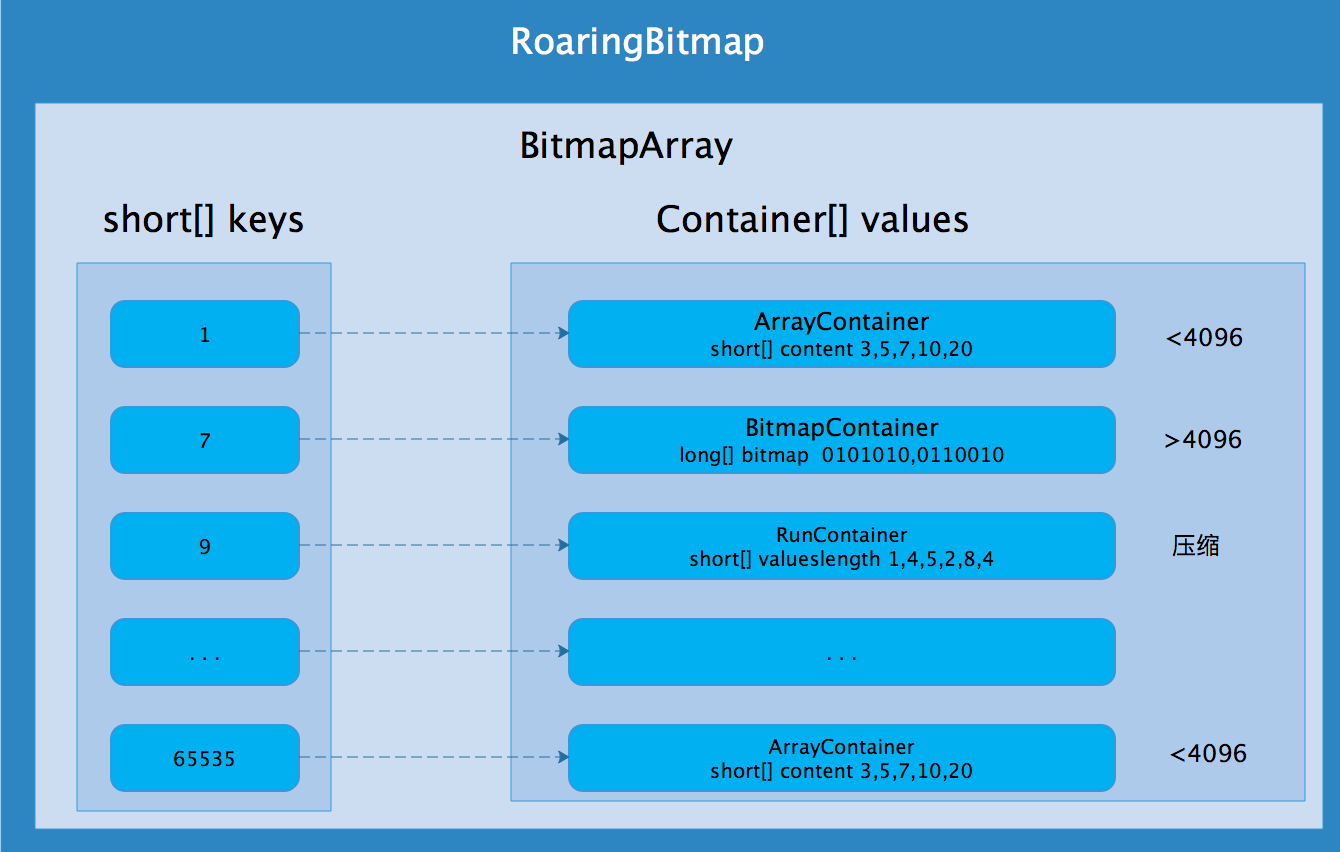
- Array Container: 变长short数组，最大容量超过4096时转换为Bitmap Container
- Bitmap Container: long数组，恒定容量为1024，固定占用内存8kb
- Run Container：边长short数组，利用行程编码数据，比如11,12,13,14将会被编码为11,3。故Run Container压缩效果最小为4b(全连续)，最大为128kb(全奇数或偶数)

实现

引入相应依赖

<dependency>
    <groupId>org.roaringbitmap</groupId>
    <artifactId>RoaringBitmap</artifactId>
    <version>0.9.47</version>
</dependency>

代码

RoaringBitmap roaringBitmap = RoaringBitmap.bitmapOf(1, 3, 3, 5);
System.out.println(roaringBitmap.getCardinality());

特点
- 对整型数据绝对精确，可以实现高效压缩
优化
- 整数超出32位整数(42亿)范围: 可以采用64位RoaringBitmap
```
Roaring64Bitmap roaring64Bitmap = RoaringBitmap.bitmapOf(1L, 3L, 3L, 5L);
System.out.println(roaring64Bitmap.getCardinality());
```
- 数据类型不是整数：采用全局字典，例如Flink + Hologres

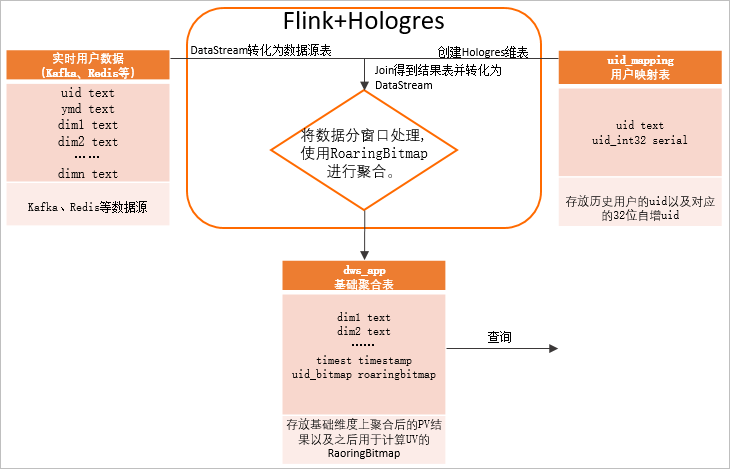
Bloom Filter

计数其实也可以转化为判断元素存在的问题，可以利用Bloom Filter数据结构。

原理：将x,y,z三个元素通过三个不同的hash函数映射到bitmap中。当查询元素w时，通过hash函数计算是否全为1，如有一个为0，则元素不在该集合中
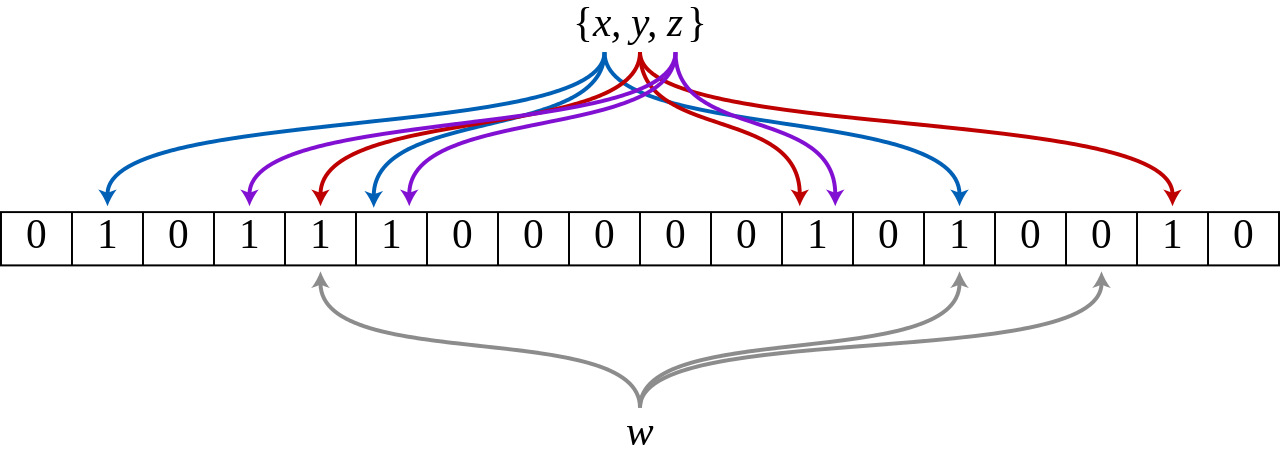
- 由于hash冲突的问题，Bloom Filter会有假阳性(False Positive), 但不会有假阴性(False Negative)

实现：

引入依赖

<dependency>
    <groupId>com.google.guava</groupId>
    <artifactId>guava</artifactId>
    <version>32.1.2-jre</version>
</dependency>

代码

/** 容量为500、百分之1假阳性的Bloom Filter */
BloomFilter<Integer> filter = BloomFilter.create(
    Funnels.integerFunnel(),
    500,
    0.01);
filter.put(1);
filter.put(3);
filter.put(5);
System.out.println(filter.mightContain(2));
System.out.println(filter.mightContain(5));

旁注: Hash冲突的概率有多大？参考生日悖论

HyperLogLog

其实在大多数数据分析中，并不要求绝对精确，这个时候就可以引入概率统计算法，追求极致的性能~

原理
- 试想在均匀分布的数据集合中，去计算数据中最大连续0出现的个数r，我们大概率会猜测这个集合的基数为2^r
- 但如果只做一次实验的话，方差会太大，所以我们采用分桶m平均的方法减少方差
  - 基数估计: |A|_{hll} = CONSTANT * m * \frac{m} {\sum_{1}^{m} 2^{-r_i}}
  - 误差服从 \sigma = 1.04 / \sqrt{m}的正态分布, 例如当 m = 2^{11} 时，99%的概率误差在7%内(3 sigma原则)
  - 存储分析：当 m=2^{11} 以及 r=5(最多记录32个0), 只需 2048 \times 5 = 1.2KB就能估计 2^{27} 的基数

实现

引入相应依赖

<dependency>
    <groupId>net.agkn</groupId>
    <artifactId>hll</artifactId>
    <version>1.6.0</version>
</dependency>

代码

HLL hll1 = new HLL(13/*log2m*/, 5/*registerWidth*/);
/** 需要先进行hash使数据均匀分布 */
hll.addRaw(1L);
hll.addRaw(3L);
hll.addRaw(5L);
System.out.println(hll1.cardinality());

特点
- 极致的性能：空间占用只需O(mlog2log2N)
- 有一定的误差

旁注：HLL的交集如何计算？可以利用容斥原理计算, 但误差会增大。

总结

本篇文章我们总结了几种常用的大数据去重统计方法，每个方法都有其适用范围，希望可以帮助大家在不同的应用场景中选择相应合适的方法~

#数据

#去重 #数据结构 #总结

大数据去重统计

https://syntomic.cn/archives/big-data-deduplication-and-statistics

作者

syntomic

发布于

2023年08月25日

更新于

2024年08月27日

许可协议

我的数据体系上一篇

Flink规则引擎下一篇