你本可以发现谱序列——Timothy Y.Chow

本文翻译自 Timothy Y.Chow文章：You Could Have Invented Spectral Sequences，旨在通过“自发现”的视角，揭示谱序列（Spectral Sequence）的本质与动机，消除其因复杂符号和索引带来的学习障碍，并展示其如何从过滤复形的自然分解中逐步涌现。

引言

谱序列这一课题对初学者而言素有艰深之名。甚至G. W. Whitehead（引自John McCleary[4]）也曾感叹："源自Lyndon和Koszul代数工作的谱序列机制，对许多拓扑学家而言显得复杂而晦涩。"

为何如此？David Eisenbud[1]提出一种解释："谱序列的课题本质上是初等的，但双复形的谱序列涉及如此多的对象与下标，乍看令人望而生畏。"我也常听到类似抱怨——上标与下标如野草般蔓生。

然而，我的解释是：谱序列的教学往往未能阐明其定义从何而来。例如，John McCleary的优秀教材[4]写道："使用者无需深究其起源，只需熟悉这些装置的操控。"但若不解其本源，谱序列自然显得神秘。反之，若能窥见其来处，符号便不再是绊脚石。

愚者总在天使畏惧处莽撞前行。因此，我的目标是让读者感到：在灵光乍现之时，你本可以发现谱序列！本文假定读者熟悉同调群，此外无需高深知识。所述内容对行家而言皆属常识，但我希望这些思想能惠及更多人——而非仅限于那些恰逢其时、恰遇其人、恰得其法的幸运儿。

对谱序列历史及其实际发明过程感兴趣的读者，可参阅文献[3]，其中给出了权威记述。

简化假设

全文在域上讨论。所有链群均为有限维，所有滤过（后文详述）仅含有限层。在"现实世界"中，这些假设或失效，但在此简化框架下，核心思想更易把握。

分级复形

"自然"出现的链复形常携带边界映射之外的额外结构。某些类型的额外结构尤为常见，因此有必要找到系统方法以利用这些特征，避免每次计算同调群时重复发明轮子。

一个简单例子：假设我们有链复形

\cdots \xrightarrow{\partial} C_{d+1} \xrightarrow{\partial} C_d \xrightarrow{\partial} C_{d-1} \xrightarrow{\partial} \cdots

且该复形是"分级"的，即每个 C_d 可分解为直和

C_d = \bigoplus_{p=1}^{n} C_{d,p}

且边界映射 \partial保分级，即对所有 d和 p，有 \partial C_{d,p} \subseteq C_{d,p-1}。此时，分级允许我们将同调计算分解为更小的部分：只需独立计算每级同调，再求和即得原复形的同调。

可惜实践中，我们并不总能幸运地拥有分级复形。更常见的是滤过(filtered)复形：即每个 C_d配备嵌套子模序列

0 = C_{d,0} \subseteq C_{d,1} \subseteq C_{d,2} \subseteq \cdots \subseteq C_{d,n} = C_d

且边界映射保滤过，即对所有 d和 p，满足

\partial C_{d,p} \subseteq C_{d-1,p} \tag{1}

（注：下标 p称为滤过度。此处其自然意义仅限 0 \le p \le n，但全文允许下标"越界"，此时相关对象视为零。例如， C_{d, -1}=0 ）

尽管滤过复形不同于分级复形，但相似性足以让我们思考：类似的"分治"策略是否适用？例如，能否自然地将滤过复形的同调群分解为直和？答案虽为肯定，但情形出人意料地复杂。下文分析将直接导向谱序列的概念。

让我们天真地尝试将问题"约化"为已解决的分级复形情形。为此，需将每个 C_d表示为直和。显然， C_d并非 C_{d,p}的直和——事实上 C_{d,n}已是整个 C_d。但由于 C_d是有限维向量空间（见初始假设），我们可通过模掉子空间 U再直和 U来获得同构空间，即 C_d \simeq (C_d/U) \oplus U。特别地，取 U = C_{d,n-1}，并迭代此过程分解 U自身，直至底层。形式化地，对所有 d和 p定义

E^0_{d,p} \overset{def} = C_{d,p}/C_{d,p-1} \tag{2}

(注意： 谱序列的索引约定存在不同版本。 多数文献中使用 E^0_{p,q}， 其中 q=d-p称为补次数，但此处为便于教学理解，采用了自认为更清晰的索引约定 。) 则

C_d \simeq \bigoplus_{p=1}^n E^0_{d,p} \tag{3}

此分解的妙处在于：边界映射 \partial自然诱导映射

\partial^0 : \bigoplus_{p=1}^n E^0_{d,p} \to \bigoplus_{p=1}^n E^0_{d-1,p}

使得所有 d和 p有\partial^0 E^0_{d,p} \subseteq E^0_{d-1,p} 。原因在于：若 C_{d,p}中两元素相差 C_{d,p-1}的元素，则根据式（1），其像再 C_{d-1,p}中相差 \partial C_{d,p-1} \subseteq C_{d-1,p-1}的元素。

于是我们得到分拆为 n部分的分级复形

\begin{array}{ccccccc} \cdots \xrightarrow{\partial^0} & E^0_{d+1,n} & \xrightarrow{\partial^0} & E^0_{d,n} & \xrightarrow{\partial^0} & E^0_{d-1,n} & \xrightarrow{\partial^0} \cdots \\ \cdots \xrightarrow{\partial^0} & E^0_{d+1,n-1} & \xrightarrow{\partial^0} & E^0_{d,n-1} & \xrightarrow{\partial^0} & E^0_{d-1,n-1} & \xrightarrow{\partial^0} \cdots \\ & \hspace{1.2em}\vdots & \hspace{1.2em}\vdots & \hspace{1.2em}\vdots & \hspace{1.2em}\vdots & \hspace{1.2em}\vdots & \\ \cdots \xrightarrow{\partial^0} & E^0_{d+1,1} & \xrightarrow{\partial^0} & E^0_{d,1} & \xrightarrow{\partial^0} & E^0_{d-1,1} & \xrightarrow{\partial^0} \cdots \end{array} \tag{4}

定义 E^1_{d,p}为该复形第 p级同调:

E^1_{d,p} \overset{\text{def}}{=} H_d(E^0_{d,p}) = \frac{\ker \partial^0 : E^0_{d,p} \to E^0_{d-1,p}}{\operatorname{im} \partial^0 : E^0_{d+1,p} \to E^0_{d,p}} \tag{5}

（熟悉相对同调的读者会注意到， E^1_{d,p}即为相对同调群 H_d(C_p,C_{p-1})。）天真地，我们希望

\bigoplus_{p=1}^n E^1_{d,p} \tag{6}

即原复形的同调。可惜这过于简单而不成立。尽管分级复形 (\bigoplus_p E^0_{d,p}, \partial^0)（称为原滤过复形的相伴分级复形）的每一项与原复形同构，但这不保证二者作为链复形同构。因此， \bigoplus_p E^1_{d,p}确为相伴分级复形的同调，却未必是原复形的同调。

差异分析

这令人略感失望，但莫轻言放弃。相伴分级复形与原复形关系密切，即便其同调非所求，亦应是良好近似。让我们仔细审视差异，探寻修补之法。

为简化讨论，先考虑 n=2的情形。此时图(4)的阵列仅含两层，称为"楼上"(p=2)与"楼下"(p=1) 。

我们真正需要的同调群是 H_d=Z_d/B_d，其中 Z_d是 C_d的闭链空间， B_d为C_d的边界空间。由于C_d是滤过的，Z_d和B_d也自然地带有滤过结构：

0 = Z_{d,0} \subseteq Z_{d,1} \subseteq Z_{d,2} = Z_d

和

0 = B_{d,0} \subseteq B_{d,1} \subseteq B_{d,2} = B_d

回想此前尝试将 H_d分解为直和地思路，正如我们之前观察到 C_d并非C_{d,1}与 C_{d, 2}的直和，现在同样发现Z_d/B_d也不是Z_{d,1}/B_{d,1}与Z_{d,2}/B_{d,2}的直和——事实上，仅Z_{d,2}/B_{d,2}本身已是完整的同调群。但我们任然可以使用同样的技巧：先对”楼下部分“取商空间，再与”楼下部分“自身直和：

\begin{aligned} \frac{Z_d}{B_d} &\cong \frac{Z_d + C_{d,1}}{B_d + C_{d,1}} \oplus \frac{Z_d \cap C_{d,1}}{B_d \cap C_{d,1}} \\ &= \frac{Z_{d,2} + C_{d,1}}{B_{d,2} + C_{d,1}} \oplus \frac{Z_{d,1}}{B_{d,1}} \end{aligned}

此时，我们天真地希望：

E_{d,2}^1 \overset{?} \simeq \frac{Z_{d,2} + C_{d,1}}{B_{d,2} + C_{d,1}} \tag{7}

和

E_{d,1}^1 \overset{?} \simeq \frac{Z_{d,1}}{B_{d,1}} \tag{8}

且方程（7）和（8）中的分子与分母恰好对应 E^1_{d,p}(见上文方程（5）)中的”闭链“和”边界“。若如此，表达式（6）将给出 H_d的直和分解。然而遗憾的是，一般情况下（7）和（8）均不成立，需进行修正。

首先观察”楼下“的 E^1_{d,1}。其”闭链“是E^0_{d,1}中的闭链，”边界“则是映射

\partial^0 : E_{d+1,1}^0 \to E_{d,1}^0

的像 I。E^0_{d,1}中的闭链空间是Z_{d,1}，即方程（8）的分子。然而，像 I并非B_{d,1}。因为B_{d,1}是B_{d}中位于C_{d,1}的部分，尽管它包含 I，但也可能包含其他元素。具体而言，映射 \partial可能将某些元素 x \in C_{d+1}从”楼上“带到”楼下“，而I仅捕获原本已在楼下的元素的边界。因此， Z_{d,1}/B_{d,1}是E^1_{d,1}的商空间。

再来看”楼下“的E^1_{d,2}。此时，”边界“空间是 B_{d,2} + C_{d, 1}（即方程（7）的分母），而”闭链“空间是映射

\partial^0 : E_{d,2}^0 \to E_{d-1,2}^0

的核 K。根据 E^0的定义，此映射为

\partial^0 : \frac{C_{d,2}}{C_{d,1}} \to \frac{C_{d-1,2}}{C_{d-1,1}}

因此， K不仅包含被 \partial映射到零的链，还包含任何被 \partial映射到”楼下“ C_{d-1,1}的链。相比之下， Z_{d,2} + C_{d,1}的元素更为特殊：它们的边界是来自 C_{d,1}的链的边界。因此，

\frac{Z_{d,2} + C_{d,1}}{B_{d,2} + C_{d,1}}

是 E_{d,2}^1的一个子空间，对应那些边界为 C_{d,1}-链边界的元素。

直观上，问题在于关联分次复形仅“感知”局限于单一水平层级的活动，而上下层级的内容被截断。但在原复形中，边界映射 \partial可能将元素下移至一个或多个层级（由于 \partial保持过滤性，不能上移），因此必须对这种跨层级活动进行修正。

谱序列的浮现

谱序列机制的精妙在于：上述对同调群​ E_{d,p}^1的修正，可视为"同调的同调"。

注意 \partial自然诱导映射（记为 \partial^1）从​ E_{d+1,2}^1到​ E_{d,1}^1，因​ E_{d+1,2}^1中元素之边界是位于 C_{d,1}的闭链，从而定义​ E_{d,1}^1的元素。对 n=2的情形，关键断言如下：

  • 断言1：如果将E_{d,1}^1模掉 \partial^1的像，即得到 Z_{d,1}/B_{d.1}。只需要去验证，\partial^1的像给出所有位于 C_{d,1}的边界。

  • 断言2：\partial^1的核是E_{d,2}^1 的子空间，同构于

\frac{Z_{d+1,2} + C_{d+1,1}}{B_{d+1,2} + C_{d+1,1}}

同样地，只需验证核仅由那些边界等于某个 C_{d+1,1}元素边界的元组成。

我们可通过下图可视化这些断言

\begin{matrix} 0 & & 0 & & 0 & & 0 & & 0 \\ & \searrow^{\partial^1} & & \searrow^{\partial^1} & & \searrow^{\partial^1} & & \searrow^{\partial^1} & \\ \cdots & & E^1_{d+1,2} & & E^1_{d,2} & & E^1_{d-1,2} & & \cdots \\ & \searrow^{\partial^1} & & \searrow^{\partial^1} & & \searrow^{\partial^1} & & \searrow^{\partial^1} & \\ \cdots & & E^1_{d+1,1} & & E^1_{d,1} & & E^1_{d-1,1} & & \cdots \\ & \searrow^{\partial^1} & & \searrow^{\partial^1} & & \searrow^{\partial^1} & & \searrow^{\partial^1} & \\ 0 & & 0 & & 0 & & 0 & & 0 \\ \end{matrix}

图(9)是一族链复形，其链复形不如图(4)般水平延伸，而是以45度角斜向下延伸，每复形仅含两个非零项。（注：本文的索引约定与多数文献不同，因此其他文献中的图表相对于图(9)会呈现“倾斜”效果。）若定义 E^2_{d,p} 为同调，即

E^2_{d,p} \overset{def} = H_d(E^1_{d,p}) = \frac{ker\partial^1: E^1_{d,p} \rightarrow E^1_{d-1,p-1}}{im\partial: E^1_{d+1,p+1} \rightarrow E^1_{d,p}}

则断言1与2表明： E^2_{d,1} \oplus E^2_{d,2}是（终于！）即为原滤过复形的正确同调。

对于 n=2，故事就此结束。序列 E^0,E^1,E^2即滤过复形的谱序列。我们可视E^1为所需同调的一阶近似，E^2为二阶近似——而当 n=2时，这不仅是近似，更是真实答案。

若 n > 2呢? 定义 (2) (5) (10) 仍成立，但E^2一般不再给出真实同调，因其仅考虑图(4)相邻层的交互作用，而 \partial能下移多层。故须考虑更高阶项 E^3,E^4,\dots,E^n。例如，定义E^3时，可验证 \partial诱导映射 \partial^2从 E^2_{d+1,p+2}到 E^2_{d,p}，类似图(9)但箭头斜降两层。一般地。对 E^r，箭头\partial^r从 E^r_{d+1,p+r}斜降 r 层至E^r_{d,p}，而 E^{r+1}定义为 (E^r,\partial^r)的同调。

验证对一般 n， H_d \simeq \oplus_p E^n_{d,p} 是前述思想的直接推广，过程繁琐故略去。

此有何用

分析学中，用级数近似逼近目标量的价值人尽皆知。当首几项已捕获大部分信息时，近似尤为宝贵。

类似评论适用于谱序列。常见现象是：当 r较小时，大量 E^r_{d,p}和/或边界映射 \partial^r为零，导致谱序列快速稳定或坍塌，从而快速地计算同调。我们通过勾勒Phil Hanlon论文[2]中定理2的证明以作说明。此例虽非谱序列的"主流"应用，却胜在无需背景知识即可理解。熟悉拓扑学的读者可以直接参考教科书中的标准例子。

设 Q为一个有限偏序集，其满足以下条件：

  • 分层性：所有极大全序子集元素数相同，故每个元素可赋予秩（即在任何包含它的极大全序子集中的位置编号）。

  • 对合性：配备一个反序对合 x \rightarrow x^*

令

\gamma = \{\alpha_1,\alpha_2,\dots,\alpha_t \} \quad \text{其中} \quad \alpha_1 < \alpha_2 < \dots < \alpha_t \tag{11}

为 Q的一个全序子集。若 \alpha_i \neq \alpha^*_j对所有 i,j成立，则称 \gamma是各向同性(isotropic)的。

向Q添加最小元 \hat{0} 和最大元 \hat{1} 后，考虑新偏序集中所有全序子集构成的抽象单纯复形 \Delta，其同调群记为 H_d。若仅限制于各向同性全序子集，则构成子复形 \Delta^0，其同调群记为 H_d^0。

Hanlon 的定理 2 指出：若 Q是Cohen-Macaulay的，且其极大全序子集有 m个元素，则当 0 \leq d \leq m/2时， H^0_d =0。此处无需深究Cohen-Macaulay的具体定义，只需知道该性质保证了某种同调特性（详见Hanlon的论文）。特别地，若 Q是Cohen-Macaulay，则可推断出 H_d的信息。

为了从H_d推导H_d^0的性质，我们需要建立二者之间的关系。Hanlon的核心思路是：对于如式（11）的 \gamma，令 \rho(\gamma)表示 \alpha_i的秩，其中 i是满足 \alpha_i^* = \alpha_j 对某 i < j的最大下标。则 \rho(\gamma) = 0当且仅当 \gamma是各向同性的。关键之处在于，应用边界映射只会降低 \rho，因此 \rho诱导了 \Delta上的一个滤过。具体来说，滤过的第 p层由满足\rho(\gamma) \leq p的 \gamma构成。由此，我们得到了一个谱序列！它建立了 H^0_d = E^1_{d, 0}与谱序列极限 H_d之间的联系。

Hanlon证明的核心在于分析 E^1。它表明，除特定 (d,p)对外， E^1_{d,p}=0。例如，当 m = 10时， E^1_{d,p}=0的例外情形如下图（以点标识）

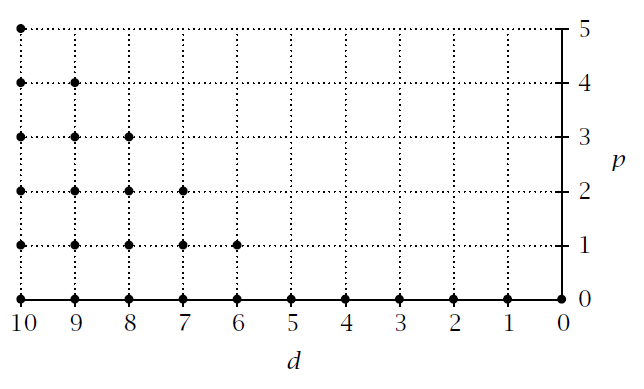
若想象斜率为 45^o的边界映射，则当 d \ge 5 = m/2时可能出现复杂情况；但对于d < m/2，所有 p对应的E^2_{d,p} 将同构于 E^1_{d,p} 。事实上，当d < m/2时，对任意 r \ge 1，均有 E^r_{d,p} \simeq E^1_{d,p}。边界映射随 r增大而愈发倾斜，但这无碍结果。因此，仅需计算 E^1即可得到某些 d值得完整同调群。特别地，当d < m/2时， H^0_d \simeq H_d。而Cohen-Macaulay条件可直接推出此时 H_d = 0，从而完成证明。

超越一瞥

当简化假设失效时，诸多复杂涌现。在任意交换环上，式(3)未必成立——并非每个短正合列可裂，故可能存在扩张问题。当有限性条件放松时，或需考虑任意大 r 的 E^r，且谱序列可能不收敛。即使收敛，亦未必收敛于目标同调。故许多应用中，现实不如前文所述轻松。然简化情形仍可视作"理想"情境，更现实情形是其扰动。

谱序列之自然性使其不仅源自滤过复形，亦见于双复形、正合偶等。虽无法在此穷尽，但愿本教程助您更有信心研读教科书。

"谱"之词源

常见疑问是"谱"字何来。此形容词源自Leray，但他未公开解释选择原因。John McCleary（私人交流）等推测：作为分析学家，Leray或视谱序列各项数据如同算子特征值般逐层揭示。若有读者知晓更多，欢迎告知。

致谢

本文初稿为1997年春我在数学科学研究所任普通成员时的讲稿，部分受NSF博士后基金资助。衷心感谢Art Duval细致校阅并提供改进建议，并多次鼓励我正式发表。感谢John McCleary指出文献[3][5]，后者亦为面向初学者的谱序列导引。最后，感谢Phil Hanlon助我理解谱序列。文中阐述之方法，他至少与我同等功劳。

参考文献

[1] DAVID EISENBUD, Commutative Algebra With a View Toward Algebraic Geometry, Springer-Verlag, 1995.

[2] PHIL HANLON, A note on the homology of signed posets, J. Algebraic Combin. 5 (1996), 245–250.

[3] JOHN MCCLEARY, A history of spectral sequences: Origins to 1953, in History of Topology, edited by Ioan M.James, North Holland, 1999, 631–663.

[4] ______ , A User’s Guide to Spectral Sequences, 2nd ed., Cambridge University Press, 2001.

[5] BARRY MITCHELL, Spectral sequences for the layman, Amer. Math. Monthly 76 (1969), 599–605.

#数学
#翻译
你本可以发现谱序列——Timothy Y.Chow
https://syntomic.cn/archives/you-could-have-invented-spectral-sequence
作者
syntomic
发布于
2025年03月30日
更新于
2025年03月30日
许可协议